Bevor es wieder an die Arbeit geht: Hast du in der Übersicht alles, was du erledigt hast, abgehakt und alle bisherigen Abschnittsberichte gewissenhaft erledigt?

In diesem Abschnitt wird es wieder sehr praktisch. Und die Mathematik der letzten Abschnitte begegnet uns dabei. Los geht es!

Du beginnst, ein Dach auf deine Garage zu bauen:

• Nimm ein Blatt aus dem Abschnitt zur Hand, fülle das Beschriftungsfeld mit 6.2 (!) aus. Du wirst es im nächsten Abschnittsbereich benötigen und schon jetzt einige wichtige Infos notieren!
• Zeichne die Diagonalen auf der Außenseite deines Schachtelbodens ein.
• Markiere den Schnittpunkt und mache ein kleines Loch. Verwende dazu die Zirkelspitze.
• Ermittle die Länge der halben Diagonale, also vom Diagonalenschnittpunkt bis zu einem Eckpunkt des Schachtelbodens.
• Notiere auf deinem Blatt die Länge der halben Diagonale.
• Hole dir ein Holzstück bei den Lehrpersonen.
• Skizziere das Holzstück auf deinem Blatt, ermittle die Länge deines Holzstückes und notiere die Länge in deiner Skizze auf dem Blatt.
• Befestige das Holzstück auf der Außenseite des Schachtelbodens: Dazu holst du dir einen Nagel und einen Hammer. Stecke den Nagel durch das Loch in der Schachtel, das du bereits gemacht hast, trage Kleber auf das Holzstück auf und befestige es schließlich auf dem Schachtelboden. Gehe vorsichtig mit dem Hammer um!

Jetzt hast du schon einen Teil deines Daches angefertigt. Im nächsten Abschnittsbereich bringst du die Sparren an:

Die sogenannten Sparren tragen dein Dach. Sie verlaufen von der Spitze des Holzstabes bis zu den Ecken des ursprünglichen Schachtelbodens. Folgendes Bild hilft dir, um zu verstehen, wie das gemeint ist:

Bevor du die Sparren (bestehend aus einer Wollschnur) anbringst, berechnest du die Länge derselben mit Hilfe des Satzes des Pythagoras:

• Dazu hast du schon zwei wichtige Infos auf deinem Blatt 6.2: Die Länge der halben Diagonale und die Länge des Holzstabes. Der Holzstab und die halbe Diagonale sind die Katheten eines rechtwinkligen Dreieckes, der Sparren ist die Hypotenuse.
• Berechne die Länge der Sparren, um herauszufinden, wie viel Material (Wolle) du für einen und für alle Sparren benötigst. Erledige alle Berechnungen auf deinem Blatt. Nutze die Tabelle, die du im Abschnitt 4.4 findest.
• Notiere am Ende deinen Materialbedarf für einen und für alle vier Sparren.

Jetzt bringst du einen Sparren an und vergleichst die berechnete Länge mit der tatsächlichen:

• Spanne deine Wollschnur von der Spitze des Holzstabes bis zur Schachtelecke.
• Wie lange ist deine Schnur? Notiere das Messergebnis auf dem Blatt 6.2.
• Vergleiche dein Rechenergebnis mit der Länge eines Schnursparrens. Stimmt deine Berechnung? Gibt es Unterschiede? Warum könnte es Unterschiede geben? Hinterlasse dazu ein kurzes Kommentar auf deinem Blatt 6.2.

Am Ende sollst du alle vier Wollsparren angebracht und gut befestigt haben, damit du im nächsten Abschnittsbereich weiterarbeiten kannst.

Jetzt deckst du dein Dach. Zunächst sollst du den Materialbedarf berechnen. Aber: Wenn du glaubst, dass du diesen Teil nicht schaffst, lässt du die Berechnung aus und deckst dein Dach ohne vorherige Rechenarbeit.

Wenn du den Materialbedarf berechnest, nimmst du ein neues Blatt aus dem Abschnitt und schreibst 6.3 in das Beschriftungsfeld. Erledige alle Berechnungen und Skizzen auf diesem Blatt. Arbeite sorgfältig und nachvollziehbar! Beantworte, wie viel Material du für das Dach benötigst bzw. wie groß die Dachfläche ist.

Zur Berechnung gibt es ein paar Tipps und wichtige Infos:

• Das Dach besteht aus 4 Dreiecken, wobei gegenüberliegende Dreiecke denselben Flächeninhalt haben. Sie sind kongruent.
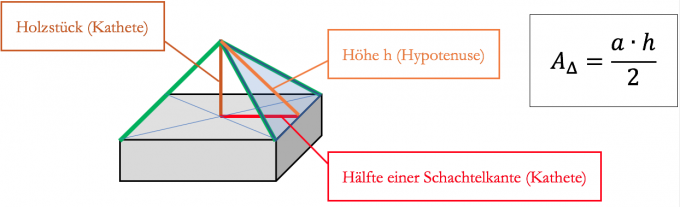
• Zur Berechnung des Flächeninhalts eines Dreieckes, benötigst du die Höhe desselben (in der folgenden Grafik orange markiert). Diese kannst du berechnen, da ein passendes rechtwinkliges Dreieck vorliegt. Du wirst wieder die Tabelle aus 4.4 benötigen.
• Dazu musst du zwei Mal den Satz des Pythagoras anwenden, da sich die Dreiecke, die das Dach später bilden, unterscheiden! Oder hast du eine quadratische Schuhschachtel? Dann wird das Dach aus vier kongruenten Dreiecken gebildet und du bist schneller am Ziel.

Hier ein paar Tipps und eine Formel. Das sollte dir helfen:

Wenn du die Berechnung erledigt hast oder sie ausgelassen hast, dann vollendest du jetzt das Dach:

• Hole dir dazu Drachenpapier (transparentes Papier) bei den Lehrpersonen und decke damit dein Dach ein.
• Arbeite sauber und denke daran: Kleber verwenden und nicht verschwenden!
• Überlege selbst, wie du das Papier am besten an den Wollsparren und an der Schachtel befestigst.

Schließe diesen Abschnitt wie immer mit dem Abschnittsbericht ab und kontrolliere auch deine Übersichtstabelle ganz vorne in der Mappe!