DEFINIZIONE CIRCONFERENZA
La circonferenza viene definita il luogo geometrico dei punti equidistanti da un punto dato detto centro e la distanza costante è il raggio.
FORMA ESPLICITA
Preso un punto C detto centro di coordinate

E un raggio di lunghezza r, possiamo l’equazione esplicita della circonferenza di centro C e raggio r è la seguente:

Per arrivare a questa formula seguiamo il seguente ragionamento:
Consideriamo un punto P(x; y) tale che appartiene alla circonferenza.
Per la definizione stessa di circonferenza questo punto deve mantenere costante la distanza dal centro e tale distanza deve essere pari al raggio.
L’equazione della circonferenza gamma che stiamo cercando si ottiene proprio imponendo che la distanza tra il punto P e il centro C è pari al raggio r.

Applicando la formula della distanza tra due punti otteniamo:

Elevando dunque entrambi i membri alla seconda otteniamo proprio l’equazione della circonferenza nella sua forma esplicita:

FORMA IMPLICITA
Partiamo dall’equazione della circonferenza nella forma esplicita:

Sviluppiamo i due quadrati di binomio:

Spostiamo tutto a sinistra e riorganizziamo i termini:

Sostituendo con:



Otteniamo l’equazione esplicita:

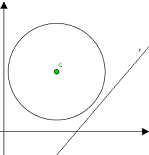
In altre parole la retta e la circonferenza non si incontrano in nessun punto, ovvero non hanno nessun punto in comune.
Il sistema, visto sopra, non ammette soluzioni e ciò si verifica quando il DISCRIMINANTE della formula risolutiva è negativo.
Δ < 0
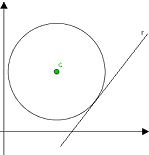
In altre parole la retta e la circonferenza hanno un solo punto in comune.
Il sistema, visto sopra, ammette una sola soluzione e ciò si verifica quando il DISCRIMINANTE della formula risolutiva è uguale a zero.
Δ = 0
In questo caso, una volta trovato il valore della x con la formula risolutiva, basta sostituirlo nell'equazione della retta per avere anche il valore della y.
I valori della x e della y trovati sono le coordinate del punto di intersezione.
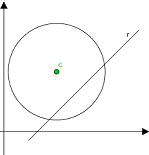
In altre parole la retta e la circonferenza hanno due punti in comune.
Il sistema, visto sopra, ammette due soluzioni e ciò si verifica quando il DISCRIMINANTE della formula risolutiva è maggiore di zero.
Δ > 0
In questo caso, una volta trovati i valori x1 e x2 con la formula risolutiva, basta sostituirli nell'equazione della retta per avere anche il valore di y1 e di y2.
Le coordinate dei due punti di intersezione saranno P1(x1 ; y2) P2(x2 ; y2).